Pular para o conteúdo principal

Circuitos Lógicos Combinacionais

Podemos aplicar diversos sinais de entrada a uma função lógica, bem como todas as suas combinações possíveis, e a expor sua saída correspondente em uma tabela. Nas colunas de entradas colocamos  todas as combinações possíveis de níveis lógicos que as entradas possam assumir. Na coluna correspondente à saída colocamos os valores que esta saída assume em função do níveis lógico correspondente.

Assim,

ENTRADAS - FUNÇÃO LÓGICA  - SAÍDA

Obviamente, a saída dependerá da função lógica utilizada (AND, OR, NOT ou XOR), conforme vimos no capítulo anterior.


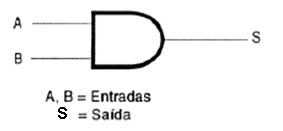
Veja, por exemplo, o caso abaixo. A e B são entradas; a função lógica é AND e a saída é S.




A
B
S   (A.B)
0
0
0
0
1
0
1
0
0
1
1
1


Agora, o que aconteceria se tivéssemos 4 entradas em uma porta AND?
Não é muito diferente do que já vimos anteriormente. Montamos a tabela verdade (24 = 16 combinações):


A
B
C
D
SAÍDA (A.B.C.D.)
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
1


...e a nossa porta lógica se pareceria com isso:


Até aqui nada de novo, mas serviu como uma boa revisão.
Agora, se eu quisesse combinar portas ou funções lógicas desta maneira....


Bom, isso é um circuito combinacional. Para elaborar a tabela verdade para este circuito e assim determinarmos todas as saídas possíveis em função das entradas, devemos levar em conta que ele é formado por duas etapas:

Na primeira etapa temos a porta AND e o inversor, enquanto que na segunda etapa temos a porta OR. Isso significa que as saídas dos circuitos da primeira etapa, que chamaremos de S1 e S2 são a entrada da segunda etapa. Temos então de levar em conta estas saídas na elaboração da tabela verdade que terá no seu topo as seguintes variáveis:

A B C S1 S2 S

Comece montando a tabela verdade das entradas A,B e C como já estamos acostumados (23 = 8 combinações):

A
B
C
S1
S2
S
0
0
0



0
0
1



0
1
0



0
1
1



1
0
0



1
0
1



1
1
0



1
1
1



A saída S1 é uma negação da entrada A, ou seja, um NOT A. Basta inverter o que a entrada A mostra:

A
B
C
S1 (NOT A)
S2
S
0
0
0
1


0
0
1
1


0
1
0
1


0
1
1
1


1
0
0
0


1
0
1
0


1
1
0
0


1
1
1
0



Agora executemos a função lógica de saída S1 que é um AND entre as entradas B e C , ou seja, B.C:

A
B
C
S1 (NOT A)
S2 (B.C)
S
0
0
0
1
0

0
0
1
1
0

0
1
0
1
0

0
1
1
1
1

1
0
0
0
0

1
0
1
0
0

1
1
0
0
0

1
1
1
0
1


...e, finalmente a saída S que uma porta OR que tem como entradas as saídas S1 e S2, ou seja, S1+S2:

A
B
C
S1 (NOT A)
S2 (B.C)
S (S1+S2)
0
0
0
1
0
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
1
1
1
1
0
0
0
0
0
1
0
1
0
0
0
1
1
0
0
0
0
1
1
1
0
1
1

Assim, temos que nosso circuito lógico combinacional tem a seguinte expressão:

S = (B.C) + A’


Exemplo 2
Vamos fazer mais um exercício para praticar. Tente fazer sozinho antes de olhar a resposta.
Vamos partir da expressão e aí construir a tabela verdade e o circuito lógico.

Expressão:
S = ABC + (A’B)

Tabela Verdade:
A
B
C
A.B.C
A’
A’B
S = ABC + (A’B)
0
0
0
0
1
0
0
0
0
1
0
1
0
0
0
1
0
0
1
1
1
0
1
1
0
1
1
1
1
0
0
0
0
0
0
1
0
1
0
0
0
0
1
1
0
0
0
0
0
1
1
1
1
0
0
1

Circuito Lógico:


Notou a “bolinha” sem preenchimento no final da entrada A? Essa é outra forma de indicar o NOT, dispensando o uso do símbolo NOT.

A pergunta que você deve estar se fazendo é como implementamos isso na prática. Bom , para isso existem os Circuitos Integrados que implementam dentro deles essas portas lógicas e é o que vamos estudar no  próximo capítulo.


Autor
Marcos Pizzolatto




Marcadores:

Comentários

Postar um comentário

Postagens mais visitadas deste blog

Transistor PUT

Vamos continuar nossos estudos sobre transistores conhecendo agora o Transistor de Unijunção Programável ou PUT. Sua função mais primitiva é gerar uma corrente de pulsos. Vamos fazer uma lista de materiais e montar dois circuitos simples usando o PUT para que você veja isso na prática e possa comparar seu funcionamento com os transistores NPN e PNP. Experimento 10.1 Lista de Material - Resistores de 20K e 100K - Capacitor eletrolítico 0,01µF - LED - 2n6027 transistor PUT - Fonte de 12 V Em nosso circuito final faremos um um led ficar piscando intermitentemente. Antes de montá-lo vamos entender o transistor programável de unijunção (PUT) e montar um circuito teste.   Observe no circuito o símbolo: Ele indica que aquele ponto deve ser ligado ao Terra ou Ground, ou simplesmente ao pólo negativo da bateria. Muitas vezes utilizado para diminuir o número de linhas do circuito para que o desenho não fique visualmente muito poluído. Eis agora , ...
Postar um comentário
Leia mais

Circuitos Integrados

O Circuito Integrado ou abreviadamente CI, é um dispositivo eletrônico que reúne diversos componentes em uma única peça e executa diversas tarefas avançadas. No entanto, se você pegar o CI de um computador, por exemplo,  e remover sua carcaça, não verá componentes comuns. Ocorre que os atuais CIs não utilizam componentes como aprendemos até agora. Tais componentes são grandes e resultariam em um CI enorme. Dê uma olhada neste CI. Eles são assim por dentro:  Neste capítulo veremos CIs que implementam funções lógica como as que estudamos nos capítulos anteriores.  Agora de uma olhada nessas duas figuras abaixo: O que você está vendo acima são dois  Circuitos Integrados  ou CI. Eles têm esse nome porque  Integram  em uma única peça funções lógicas. Na primeira imagem (7408) repare que os terminais dos componentes correspondem a 4 portas AND, enquanto a segunda figura (7432) tem representadas 4 portar OR. Os outros pinos são o ter...
Postar um comentário
Leia mais

Eletrônica Digital :Álgebra de Boole

George Boole (1814-1864), matemático e filósofo britânico, no século XIX investigou as leis fundamentais das operações da mente humana ligadas ao raciocínio e criou a Álgebra  Booleana, base da atual aritmética computacional. Enquanto que a álgebra tradicional opera com relações quantitativas, a álgebra de Boole opera com relações lógicas. Enquanto que na álgebra tradicional as variáveis podem assumir  qualquer valor, na álgebra booleana, as variáveis, aqui denominadas por variáveis binárias, apenas podem assumir um de dois valores binários, “ 0”  ou “ 1” . Estes valores binários não exprimem quantidades, mas apenas, e somente, estados do sistema. Vamos simplificar isso. Dê uma olhada no circuito abaixo. Nele existem quatro interruptores e uma lâmpada. Quando essa lâmpada irá acender? Ora, ela só irá acender quando todos os interruptores estiverem ligados. Neste circuito cada interruptor só pode apresentar uma de duas posições: ligado ou desligado. Ago...
Postar um comentário
Leia mais